Математические методы

Одной из задач, решаемых группой, является популяризация и развитие метода статистической регуляризации, созданного В.Ф. Турчиным в 70-х годах XX века.

Типичной некорректной обратной задачей, возникающей в физике, является уравнение Фредгольма I рода:

$$f(y) = \int \limits_a^b dx K(x,y)\varphi(x)$$

Фактически, это уравнение описывает следующее: аппаратная функция прибора $K(x,y)$ действует на исследуемый спектр или иной входной сигнал $\varphi$, в результате чего исследователь наблюдает выходной сигнал $f(y)$. Целью исследователя является восстановить сигнал $\varphi$ по известным $f(y)$ и $K(x,y)$. Казалось бы, восстановление сигнала не является сложной задачей, поскольку уравнение Фредгольма имеет точное решение. Но уравнение Фредгольма некорректно — бесконечно малое изменение начальных условий приводит к конечному изменению решения. Таким образом, наличие шумов, присутствующих в любом эксперименте, обесценивает попытки решить это уравнение точно.

Теория

Рассмотрим некую алгебраизацию уравнения Фредгольма:

$$f_m = K_{mn}\varphi_n$$

С точки зрения математической статистики мы должны оценить $\vec{\varphi}$ по реализации $\vec{f}$, зная плотность вероятности для $\vec{f}$ и содержимое матрицы $K$. Действуя в духе теории принятия решений, мы должны выбрать вектор-функцию $\vec{S}$, определяющую $\vec{\varphi}$ на основе $\vec{f}$ и называемую стратегией. Для того чтобы определить, какие стратегии более оптимальные, мы введем квадратичную функцию потерь:

$$L\left(\hat{\varphi},\vec{S}\right) = \left(\hat{\varphi}-\vec{S}\right)^2,$$

где $\hat{\varphi}$ — наилучшее решение. Согласно байесовскому подходу рассмотрим $\vec{\varphi}$ как случайную переменную и переместим нашу неопределенность о $\vec{\varphi}$ в априорную плотность $P(\vec{\varphi})$, выражающую достоверность различных возможных законов природы и определяемую на основе информации, сущетсвующей до проведения эксперимента. При таком подходе выбор оптимальной стратегии основывается на минимизации апостериорного риска:

$$r_{\vec{S}}(\vec{\varphi}) \equiv E_{\vec{\varphi}}E_{\vec{f}}\left[L\left(\vec{\varphi},\vec{S}\right)|\vec{\varphi}\right]$$

Тогда оптимальная стратегия в случае квадратичной функции потерь хорошо известна:

$$S^{opt} _n= E\left[\varphi_n|\vec{f}\right] = \int \varphi_n P\left(\vec{\varphi}|\vec{f}\right)d\vec{\varphi}$$

Апостериорная плотность $P(\vec{\varphi}|\vec{f})$ определяется по теореме Байеса:

$$P\left(\vec{\varphi}|\vec{f}\right)= \frac{P(\vec{\varphi})P\left(\vec{f}|\vec{\varphi}\right)}{\int d\vec{\varphi}P(\vec{\varphi})P\left(\vec{f}|\vec{\varphi}\right)}$$

Кроме того, такой подход позволяет определить дисперсию полученного решения:

$$\left\langle \sigma_n^2 \right\rangle = \int \left(\varphi_n - S^{opt}_n\right)^2 P\left(\vec{\varphi}|\vec{f}\right)d\vec{\varphi}$$

Мы получили решение, введя априорную плотность $P(\vec{\varphi})$. Можем ли мы сказать, что-либо о том мире функций $\varphi(x)$, который задается априорной плотностью? Если ответ на этот вопрос отрицательный, то мы должны будем принять все возможные $\varphi(x)$ равновероятными и вернуться к нерегуляризованному решению. Таким образом, мы должны ответить на этот вопрос положительно. Именно в этом заключается метод статистической регуляризации — регуляризация решения за счет введения дополнительной априорной информации о $\varphi(x)$. Если исследователь уже обладает какой-либо априорной информацией (априорной плотностью $P(\vec{\varphi})$), он может просто вычислить интеграл и получить ответ. В случае, если такой информации нет, в следующем параграфе описывается, какой минимальной информацией может обладать исследователь и как её использовать для получения регуляризованного решения.

Априорная информация

Как показали британские ученые, во всем остальном мире любят дифференцировать. Причем, если математик будет задаваться вопросами о правомерности этой операции, то физик оптимистично верит, что законы природы описываются «хорошим» функциями, то есть гладкими. Иначе говоря, он назначает более гладким $\varphi(x)$ более высокую априорную плотность вероятности. Так давайте попробуем ввести априорную вероятность, основанную на гладкости. Для этого мы вспомним, что введение априорной информации — это некоторое насилие над миром, принуждающее законы природы выглядеть удобным для нас образом. Это насилие следует свести к минимуму, и, вводя априорную плотность вероятности, необходимо, что бы информация Шеннона относительно $\varphi(x)$, содержащаяся в $P(\vec{\varphi})$, была минимальной. Формализуя выше сказанное, выведем вид априорной плотности, основанной на гладкости функции. Для этого мы будем искать условный экстремум информации:

$$I[P(\vec{\varphi})] = \int \ln{P(\vec{\varphi})} P(\vec{\varphi}) d\vec{\varphi} \to min$$

При следующих условиях:

1. Условие на гладкость $\varphi(x)$. Пусть $\Omega$ — некоторая матрица, характеризующая гладкость функции. Тогда потребуем, чтобы достигалось определённое значение функционала гладкости:

$$\int (\vec{\varphi},\Omega\vec{\varphi}) P(\vec{\varphi}) d\vec{\varphi} = \omega$$

Внимательный читатель должен задать вопрос об определении значения параметра $\omega$. Ответ на него будет дан далее по тексту.

2. Нормированность вероятности на единицу:

$$\int P(\vec{\varphi}) d\vec{\varphi} = 1$$

При этих условиях доставлять минимум функционалу будет следующая функция:

$$P_{\alpha}(\vec{\varphi}) = \frac{\alpha^{Rg(\Omega)/2}\det\Omega^{1/2}}{(2\pi)^{N/2}} \exp\left(-\frac{1}{2} (\vec{\varphi},\alpha\Omega\vec{\varphi})\right)$$

Параметр $\alpha$ связан с $\omega$, но поскольку у нас нет собственно информации о конкретных значениях функционала гладкости, выяснять, как именно он связан, бессмысленно. Что же тогда делать с $\alpha$, спросите вы? Здесь перед вами раскрываются три пути:

1. Подбирать значение параметра $\alpha$ вручную, и тем самым перейти к регуляризации Тихонова
2. Усреднить по всем возможным $\alpha$, предполагая все возможные $\alpha$ равновероятными
3. Выбрать наиболее вероятное $\alpha$ по его апостериорной плотности вероятности $P(\alpha|\vec{f})$. Этот подход верен, если мы предполагаем, что в экспериментальных данных содержится достаточно информации об $\alpha$.

Первый случай нам малоинтересен. Во втором случае мы получим следующую формулу для решения:

$$\left\langle \varphi_i \right\rangle = \frac{\int d\varphi\, \varphi_i P(f|\varphi) \int\limits d\alpha\,P(\alpha) \alpha^{\frac{Rg(\Omega)}{2}} \exp\left(-\frac{\alpha}{2} (\vec{\varphi},\Omega\vec{\varphi})\right)}{\int d\varphi P(f|\varphi) \int\limits d\alpha\,P(\alpha) \alpha^{\frac{Rg(\Omega)}{2}} \exp\left(-\frac{\alpha}{2} \left(\vec{\varphi},\Omega\vec{\varphi}\right)\right)}$$

Третий случай будет рассмотрен в следующем разделе на примере гауссовых шумов в эксперименте.

Случай гауссовых шумов

Случай, когда ошибки в эксперименте распределены по Гауссу, замечателен тем, что можно получить аналитическое решение нашей задачи. Решение и его ошибка будут иметь следующий вид:

$$\vec{\varphi} = \left(K^T\Sigma^{-1}K +\alpha^*\Omega\right)^{-1}K^T\Sigma^{-1^{T}}\vec{f}$$ $$\Sigma_{\vec{\varphi}} = \left(K^T\Sigma^{-1}K+\alpha^*\Omega\right)^{-1}$$

где $\Sigma$ — ковариационная матрица многомерного распределения Гаусса, $\alpha^*$ — наиболее вероятное значение параметра $\alpha$, которое определяется из условия максимума апостериорной плотности вероятности:

$$P\left(\alpha|\vec{f}\right) = C39; \alpha^{\frac{Rg(\Omega)}{2}}\sqrt{\left|\left(K^T\Sigma^{-1}K+\alpha\Omega\right)^{-1}\right|}\exp\left(\frac{1}{2} \vec{f}^T\Sigma^{-1}K^{T}(K^T\Sigma^{-1}K+\alpha\Omega)^{-1}K^T\Sigma^{-1^{T}}\vec{f}\right)$$

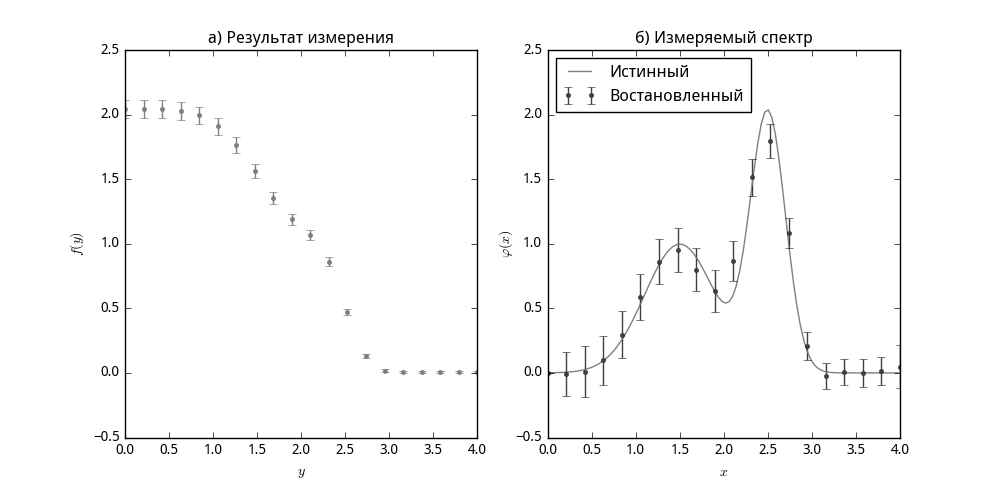
В качестве примера рассмотрим восстановление спектра, состоящего из двух гауссовых пиков, которые попали под действие интегрального ядра-ступеньки (функции Хевисайда).

Этот раздел дорабатывается...