A criterion for infinite positron feedback in Relativistic Feedback Discharge Model
Terrestrial Gamma-ray Flashes (TGF) - short (~ 100 μs) and intense flashes of terrestrial gamma radiation, the source of which is thunderstorms. This remarkable natural phenomenon has been observed for over 20 years from satellites (for example, Fermi), as well as ground-based observatories (for example, the Array telescope).
It is believed that the source of gamma radiation is avalanches of runaway electrons accelerated by thunderstorm electric fields.
Joseph Dwyer proposed a model of runaway electron avalanches - the Relativistic Feedback Discharge Model (RFDM). According to Dwyer, there is a feedback mechanism in the dynamics of avalanches, which leads to the reproduction of avalanches and, therefore, their endless existence. Such an amazing process is caused by the creation of positrons by the bremsstrahlung of electron avalanches.
In this work, an analytical study of RFDM is carried out. The spatial distributions of particles were obtained for all generations of self-replicating avalanches. And also a criterion for the existence of positron infinite feedback in thunderclouds is derived. The results are confirmed by simulation on Geant4.
The criterion can be formulated as follows. In a cell with a uniform critical electric field, the process of infinite multiplication of runaway electron avalanches due to positron feedback is possible if the following inequality is satisfied:
| {\Gamma = \frac{P \lambda_{RREA} \lambda_{-}}{(\lambda_- + \lambda_{RREA}) \lambda_2 \lambda_{\gamma} \lambda_{\gamma \rightarrow e^-e^+} cos\alpha} \left(\frac{\lambda_{RREA} \lambda_{x}}{\lambda_{x} - \lambda_{RREA}}\right)^2 \left( e^{\frac{L(\lambda_{x} - \lambda_{RREA})}{\lambda_x\lambda_{RREA}}} - 1 - \frac{L(\lambda_{x} - \lambda_{RREA})}{\lambda_x\lambda_{RREA}} \right) > 1} |
- {P = P_{e^+ reversal} \cdot P_{e^- reversal}} - the total probability of reversals (product, since the reversal of the electron and the reversal of the positron, are independent). A reversal is a reversal + runaway.
- {\lambda_{RREA}} - the length of the exponential rise of RREA.
- {\lambda_{x}} - is the path length of the positron before annihilation. Also, this number effectively takes into account the acceleration of the positron.
- {\lambda_{\gamma}} - is the path length of a runaway electron before the production of a gamma quantum with energy sufficient for the production of an electron-positron pair.
- {\lambda_{\gamma \rightarrow e^+e^-}} - is the mean free path of gamma before the birth of a positron (electron-positron pair).
- {\alpha} - the average angle relative to the z-axis, at which the gamma is flying.
- {\lambda_{2}} - is the path length of the positron before the birth of the runaway electron.
- {L} - cell length.
- {\lambda_{-}} - the length of exponential decay of gamma-ray flux.
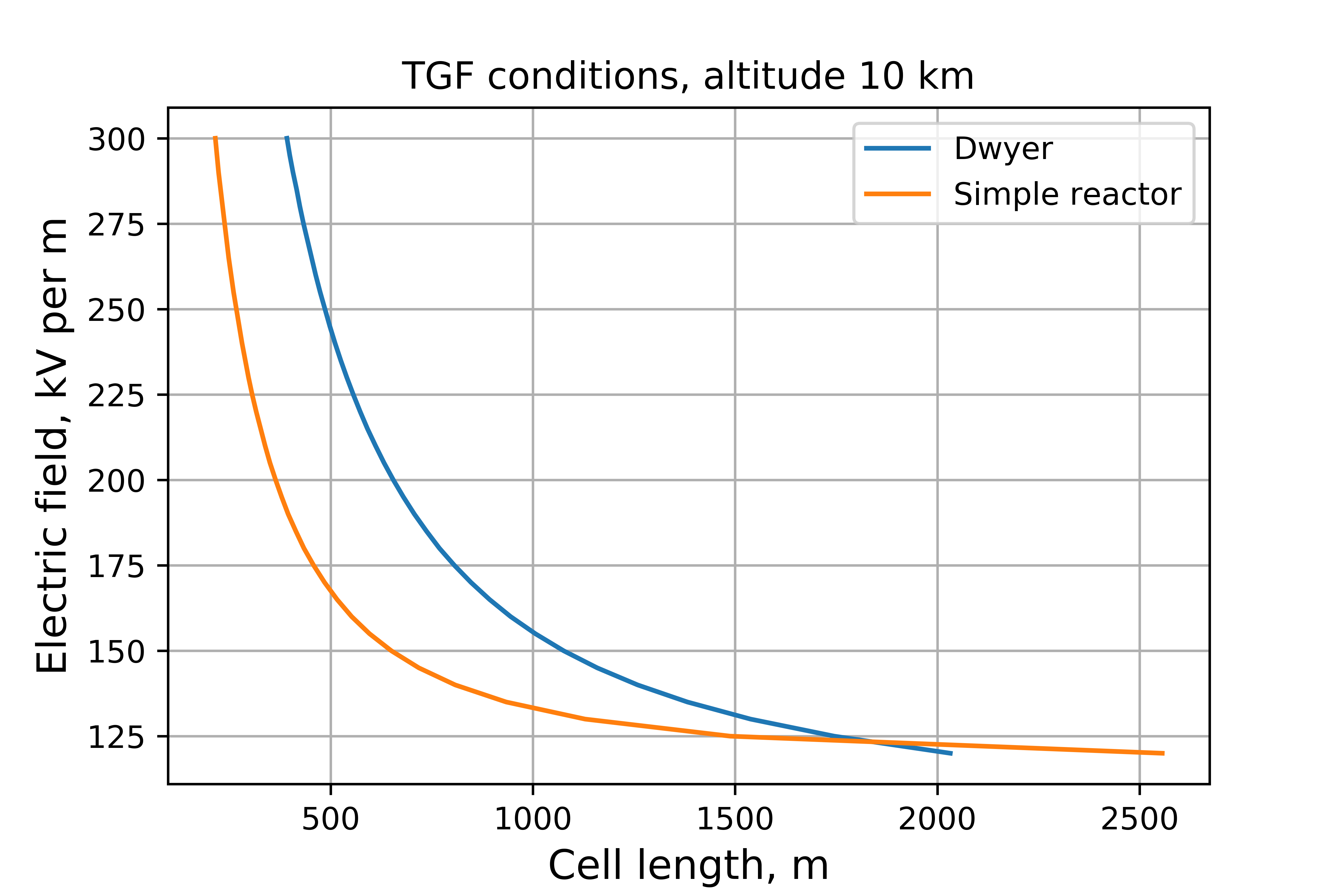
From the criterion, the conditions for the occurrence of TGF in the Dwyer model are obtained. They are shown in the figure:
Simple reactor model
High-energy atmospheric physics is attracting more and more attention from that part of the scientific community that deals with atmospheric electricity. It is believed that runaway electron avalanches accelerated by an electric field in thunderstorm clouds can play a significant role in thunderstorm phenomena. In addition, it has been reliably established that it is the process of acceleration of relativistic particles during a thunderstorm that underlies such a mysterious natural phenomenon as Terrestrial Gamma-ray Flashes (TGF).
The mere existence of runaway electron avalanches in a thundercloud is not enough for the formation of a TGF. It turns out that in order to create a powerful and simultaneously short flux of gamma radiation, experimentally observed from space, some mechanism of additional generation of relativistic electron avalanches is needed. A possible way to increase the flow of particles in avalanches is the presence of a feedback mechanism in their dynamics. The first feedback model was proposed by Joseph Dwyer. However, Dwyer's infinite feedback requires too high large-scale atmospheric electric fields.
A new model of the dynamics of runaway electron avalanches with feedback was proposed, which was named the reactor model. Its essence lies in the fact that additional amplification of the avalanches of relativistic particles in thunderstorm electric fields is possible due to their inhomogeneity. It is shown that, in an inhomogeneous field, cells with a quasi-uniform electric field exchange gamma radiation with each other, which leads to an overall increase in the flux of high-energy particles.
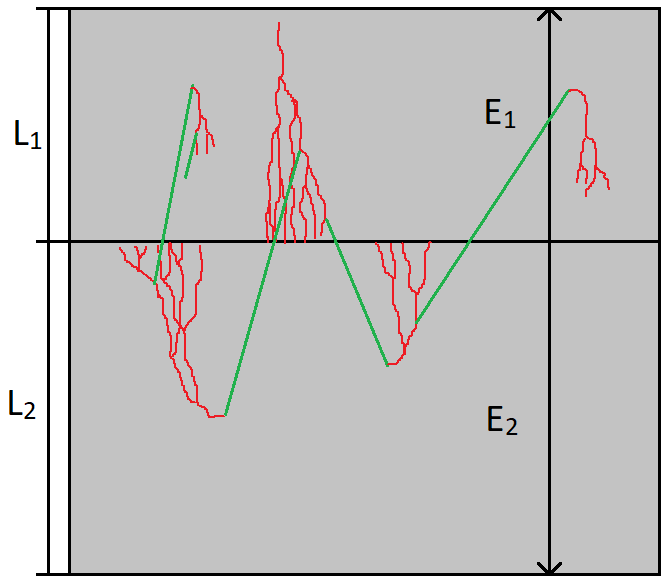
Let's consider the case of the simplest reactor: when two cells look at each other. This model is interesting for its simplicity, as well as its feasibility within the framework of generally accepted models of the structure of the electric field in thunderclouds.
In this system, gamma quanta will make an overwhelming contribution to the feedback. Let us assume that an avalanche of runaway electrons has arisen in the upper cell. This avalanche, in the course of its development, will emit inhibitory gammas that are capable of penetrating the second cell. In the second cell, as the gamma spreads, secondary electrons will be generated, which have a chance to turn around and give birth to secondary avalanches. These avalanches, in turn, emit new scales, thereby looping the process.
Why is the contribution from the electrons of the primary avalanche entering the second cell neglected? Suppose that the runaway electron accelerated in the first cell and hit the second. The second cell field will direct it back to the first. However, upon returning to the first cell, the electron ultimately does not receive energy from the field of the second cell, since its potential energy in the second field will not change. But in this case, the electron will lose energy to interact with air. Therefore, the transport of electrons from cell to cell inevitably leads to their decay, in contrast to the transport of gamma.
Let {\lambda_ {RREA} ^ i} be the avalanche growth length of runaway electrons, {\lambda _ {\gamma} ^ i} be the runaway electron free path before the emission of a gamma quantum with supercritical energy, {\lambda_ {e^-} ^ i} is the path length of the gamma before the birth of a runaway electron, and {P ^ i} is the probability of an electron turn with the further development of an avalanche of runaway electrons. These parameters depend on the magnitude of the electric field and air density. For generality, it is assumed that different cells have different fields, densities, and cell lengths.
Let {\nu_ {i}} be the amount of gamma emitted by the {i} -th cell when 1 gamma quantum from another cell gets into it. A simple kinetic calculation leads to the formula:
| {\nu^i = P^i \frac{\lambda_{RREA}^i}{\lambda_{\gamma}^i(\lambda_{RREA}^i + \lambda_{e^-}^i)} \left[ \frac{\lambda_{RREA}^i \lambda_{e^-}^i}{\lambda_{e^-}^i - \lambda_{RREA}^i} \left( e^{L^i\frac{\lambda_{e^-}^i - \lambda_{RREA}^i}{\lambda_{RREA}^i\lambda_{e^-}^i}} - 1\right) - \frac{\lambda_{e^-}^i}{2} \left( e^{-2\frac{L^i}{\lambda_{e^-}^i}} - 1\right)\right]} |
Hence, it is easy to guess that the overall amplification factor of the flux of relativistic particles in the system under consideration will be as follows:
| {\varepsilon = \nu^1 \cdot \nu^2} |
If {\varepsilon> 1} then a TGF will appear in the reactor, and an exponential growth of high-energy particles with time will be observed, approximately, in the following way:
| {N(t) = N_0 \cdot e^{\frac{c}{L_1 + L_2} \varepsilon t}} |
These formulas show a very interesting result. It turns out that even in such a simple reactor model, more realistic electric fields are required to generate TGF than in Dwyer's model. For example, if a thunderstorm cloud is at an altitude of 10 km, then in the Dwyer model, a uniform field with a strength of 200 kV per m with a length of about 750 meters is required. In such a simple reactor, two cells with a uniform field facing each other are required, each of which has a voltage of 200 kV per meter and a length of 350 meters. Within the framework of the generally accepted layered structure of thunderstorm electric fields, the scenario with the simplest reactor is more realizable.
Spatio-temporal picture in the Gurevich model
Assumptions:
- All runaway electrons move with the same speed υ along the z-axis against a uniform electric field.
- Avalanches of runaway electrons are localized strictly inside the cell.
- The cell width is much larger than the runaway electron avalanche width.
Let an avalanche of runaway electrons be generated at the point {z_0} at the time {t_0}. Then its space-time distribution will be as follows:
| {f_{RREA}(z, t, z_0, t_0) = e^{\nu (t - t_0)} \delta\left( (z - z_0) - \upsilon(t - t_0) \right) S(z) S(L - z)} |
Where {\nu = \frac{\lambda_ {RREA}}{\upsilon}} is the reproduction rate of runaway electrons, {\delta} is the Dirac delta function, {S} is the Heaviside step function, L - cell length.
Let a source of seed electrons be located at the point {z_0}, which generates {N} electrons per unit time along the {z} axis against the electric field.
Then, at the point {z} at time {t}, there will be the following number of runaway electrons:
| {F(z, t, z_0) = N e^{\frac{\nu}{\upsilon}(z - z_0)} S\left(\frac{z - z_0}{\upsilon}\right) S\left(t - \frac{z - z_0}{\upsilon}\right)} |
Suppose that seed electrons are generated uniformly along the cell. Then, at the point {z}, {N} electrons are produced per unit time. It should be noted that {N} here differs from the previous {N} in dimension.
In the case under consideration, at the point {z} at time {t} there will be the following number of runaway electrons:
| {F(z, t) = N \lambda_{RREA} S(L - z) S(z) \left[ (e^{\nu t} - 1) S(z - \upsilon t) + (e^{\frac{z}{\lambda_{RREA}}} - 1) S(\upsilon t - z) \right]} |
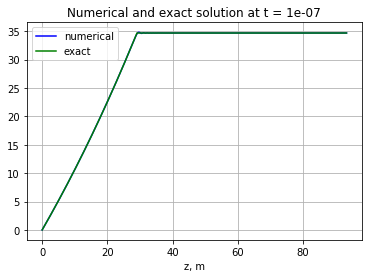
For the space-time distribution in the latter case, the following equation was also numerically solved:
| {\frac{\partial F}{\partial z} + \frac{1}{\upsilon}\frac{\partial F}{\partial t} = \frac{1}{\lambda_{RREA}} F + N(t,z)} |
- {F(t, z)} is the number of runaway electrons.
- {N(t, z)} - source function.
- {\upsilon} - runaway electron velocity.
- {\nu_f = \frac {\upsilon} {\lambda_ {RREA}}} is the multiplication frequency of runaway electrons.
The numerical solution coincided with the analytical one, and its result is shown in the figure: